Markowitz y la Teoría Moderna de Carteras

La Teoría Moderna de Carteras se define como el conjunto de aportaciones teóricas que buscan dar solución al problema de seleccionar las mejores combinaciones de activos para formar una cartera de inversión. Actualmente, los modelos que la conforman continúan siendo una referencia para muchos inversores, sin embargo, con el paso del tiempo han ido surgiendo distintas corrientes que ponen en duda su fiabilidad. Nos enfrentamos a este problema con una serie de artículos, preparados por Gabriela de la Torre, autora del proyecto Value4all, con el apoyo de Jaime Lasheras, asesor externo del proyecto.

El origen de la Teoría Eficiente de Cartera se remonta a 1952 con la Teoría del Portafolio de Harry Markowitz (1927 – 2023), galardonado con el Premio Nobel de Economía en 1990, y a quien dedicamos esta entrada del blog, en la semana antes de que se publique el Premio de 2023.

La teoría de Markowitz aboga por la diversificación de los activos como forma de reducir el riesgo. Describe al ser humano como un ser racional y, por ende, averso al riesgo. Esta teoría supuso un antes y un después en el mundo de la inversión, pues fueron sus contribuciones las sentaron las bases sobre las que se desarrollaron los primeros modelos de gestión de activos.

En 1963, en la revista académica The Journal of Finance con el artículo “A Simplified Model for Portfolio Analysis”, el economista William Sharpe dio a conocer una simplificación del modelo propuesto por Markowitz y el cuál recibió el nombre de Sharpe Diagonal Model. Posteriormente, dicho modelo fue profundizado y enriquecido por otro de sus trabajos: “Capital Asset Prices: A Theory of Market Equilibrium under Condition of Risk” (1964); que junto con las aportaciones de John Lintner (1965), Jack L. Treynor (1961), Jan Mossin (1966) y Merton Miller condujo a la aparición del modelo de valoración de activos financieros, comúnmente conocido como CAPM.

El CAPM supuso un paso más adelante en el mundo de las inversiones al buscar maximizar el rendimiento de cada activo a partir de sus datos históricos. A diferencia del modelo propuesto por Markowitz, el riesgo ya no aparecía representado por la desviación estándar, sino que introdujo un nuevo parámetro: la beta. Dicho parámetro se utilizaba como medida de correlación entre el mercado y el título en cuestión; focalizándose únicamente en el riesgo sistemático. Introdujo así la distinción entre riesgo sistemático y no sistemático, entendiendo al primero como el único posible de reducir y siendo la diversificación la única forma de conseguirlo.

Años más tarde, dos profesores de la universidad de Chicago, Eugene Fama y Kenneth French propusieron un nuevo modelo compuesto por tres factores. Según su artículo “The Cross-Section of Expected Stock Returns” publicado en la revista académica The Journal of Finance (1992), el parámetro beta no era una medida suficiente para el cálculo de la rentabilidad de un activo. De esta manera, introdujeron dos nuevas variables que representaban al tamaño y a la ratio Book-to-Market equity; posteriormente propondrían un modelo compuesto por cinco factores (2015).

En este conjunto de artículos se expone únicamente el modelo de tres factores, el cual considera una serie de factores de riesgo que pretenden capturar en mejor medida los ciclos económicos, la inflación, etc. A partir de una comparación con los modelos mencionados previamente (CAPM, Markowitz), se estudiará si estos cambios introducidos se ven reflejados en el cálculo de los rendimientos de manera favorable o, por el contrario, no suponen ninguna mejora.  

¿Por qué es importante la gestión de la cartera?

Con el transcurso de los años, son más las personas que se suman a la opción de invertir sus ahorros en el mercado de valores en vista a la posibilidad de que el sistema de pensiones no sea capaz de mantenerse o que la inflación empeore con el tiempo. Por ejemplo, en el caso de España, en 2015 el déficit del Sistema de la Seguridad Social alcanzó un 1,5% del PIB mientras que, en 2007, antes de la crisis económica, presentaba un superávit del 2,2% del PIB. Este declive se debió a una gran subida en la tasa de desempleo, pero también a causa de un incremento en el gasto de pensiones contributivas al producirse un aumento de la población en edad de jubilación. Como solución a este problema, países como Francia, han decidido prolongar la edad de jubilación y en su caso, aplazarla de los 62 a los 64 años.

Por otra parte, la inflación es una realidad, lo genera dudas sobre el valor de los ahorros para el futuro; situación que conduce al ciudadano a buscar alternativas como, por ejemplo, la inversión.

En el caso de elegir esta opción, el inversor puede decidir tomar las decisiones por sí mismo o dejar su dinero en manos de profesionales; llevar a cabo un seguimiento continuo o dejar pasar los años y esperar a retirar el capital invertido; reinvertir los dividendos o ir recibiendo una cierta cantidad cada cierto tiempo, etc. Son muchas las decisiones que debe tomar un inversor, fundamentalmente ligadas a sus conocimientos y a su aversión al riesgo. En términos del largo plazo, actualmente se tiende a asociar la gestión pasiva como mejor estrategia de inversión de cara al futuro. Este tipo de gestión se basa en replicar la rentabilidad de un índice de mercado específico sin evidentemente, poder superarlo.

Sin embargo, existen numerosos profesores e inversores que proponen la gestión activa como una mejor opción, es decir, la selección de los activos que formarán parte de la cartera por parte del propio inversor. Además, existen distintas estrategias para llevar a cabo este tipo de gestión, tales como el Value Investing, el Growth Investing o el Buy&Hold. El proyecto Value4all aboga por la estrategia de Buy&Hold, comprando empresas de calidad, estables y que repartan dividendo. Ya se ha visto que carteras sencillas creadas con este concepto son capaces de batir al mercado, como se demuestra aquí y aquí.

Pero, ¿es esa distribución sencilla la mejor? ¿O se pueden obtener mejores resultados usando una distribución de las empresas en cartera siguiendo alguna otra recomendación? Para ello, estudiaremos las distintas posibilidades que hay.

El modelo de la Teoría Moderna de Carteras

En 1952, el economista estadounidense Harry Markowitz presenta la Teoría Moderna de Carteras, un modelo con el que defiende la posibilidad de obtener una mayor rentabilidad eligiendo una cartera bien diversificada frente a elegir acciones individuales o incluso, con la compraventa de activos a corto plazo. 

Markowitz expuso su idea en el Journal of Finance, idea que posteriormente se convertirá en la base del Modelo de Valoración de Activos Financieros o “Capital Assets Pricing Model” (CAPM). Dicha idea surgió a la hora de estudiar la distribución de los cambios diarios en los precios de una acción en dónde se observó que, durante periodos pequeños la distribución se podía aproximar a la normal. Esto último permitía a los inversionistas tener en cuenta solamente dos parámetros: el rendimiento esperado y la varianza o desviación estándar. Por esta razón, el modelo de Markowitz es a su vez conocido como el Modelo Media-Varianza o como el origen de la teoría moderna de carteras.

Su objetivo persigue la aversión del riesgo a fin de maximizar el rendimiento. El riesgo aparece representado por la desviación estándar y, por consiguiente, un aumento de ésta conduce a una mayor incertidumbre y a la posibilidad de no obtener los resultados deseados.

La diversificación de carteras defendida por Markowitz permitía observar variaciones en las desviaciones y en los rendimientos al hacer combinaciones de las acciones. Partiendo de un ejemplo con 2 acciones, cada una con su rendimiento y desviación respectivos, se generan diferentes casos en los que se varía la proporción invertida en cada activo. Obteniendo así, una serie de valores para el rendimiento y la desviación en cada ejemplo.

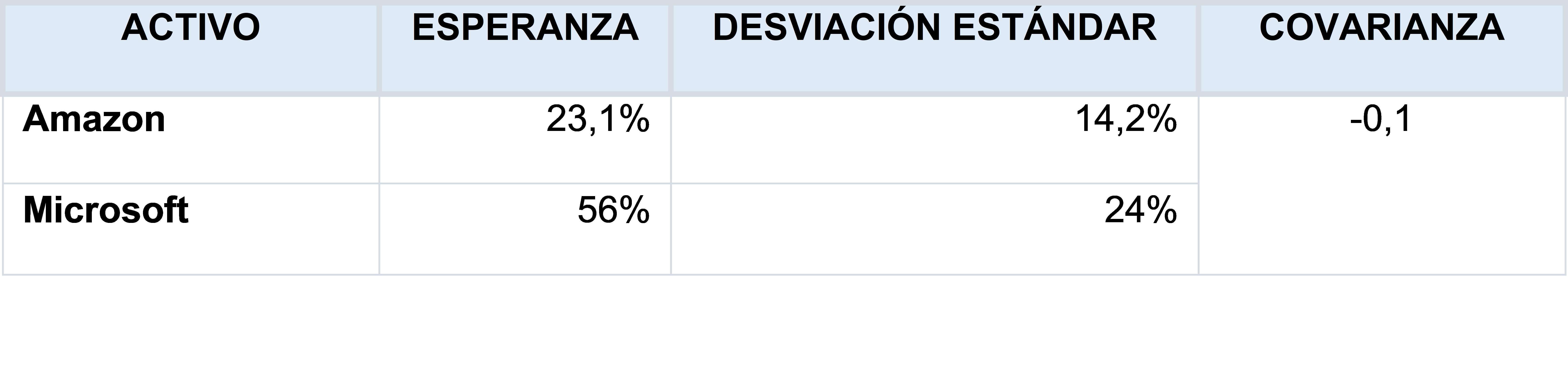
Tabla 1: Esperanza y desviación estándar de dos activos de ejemplo. Fuente: (Allen, Brealey, y Myers 2010).

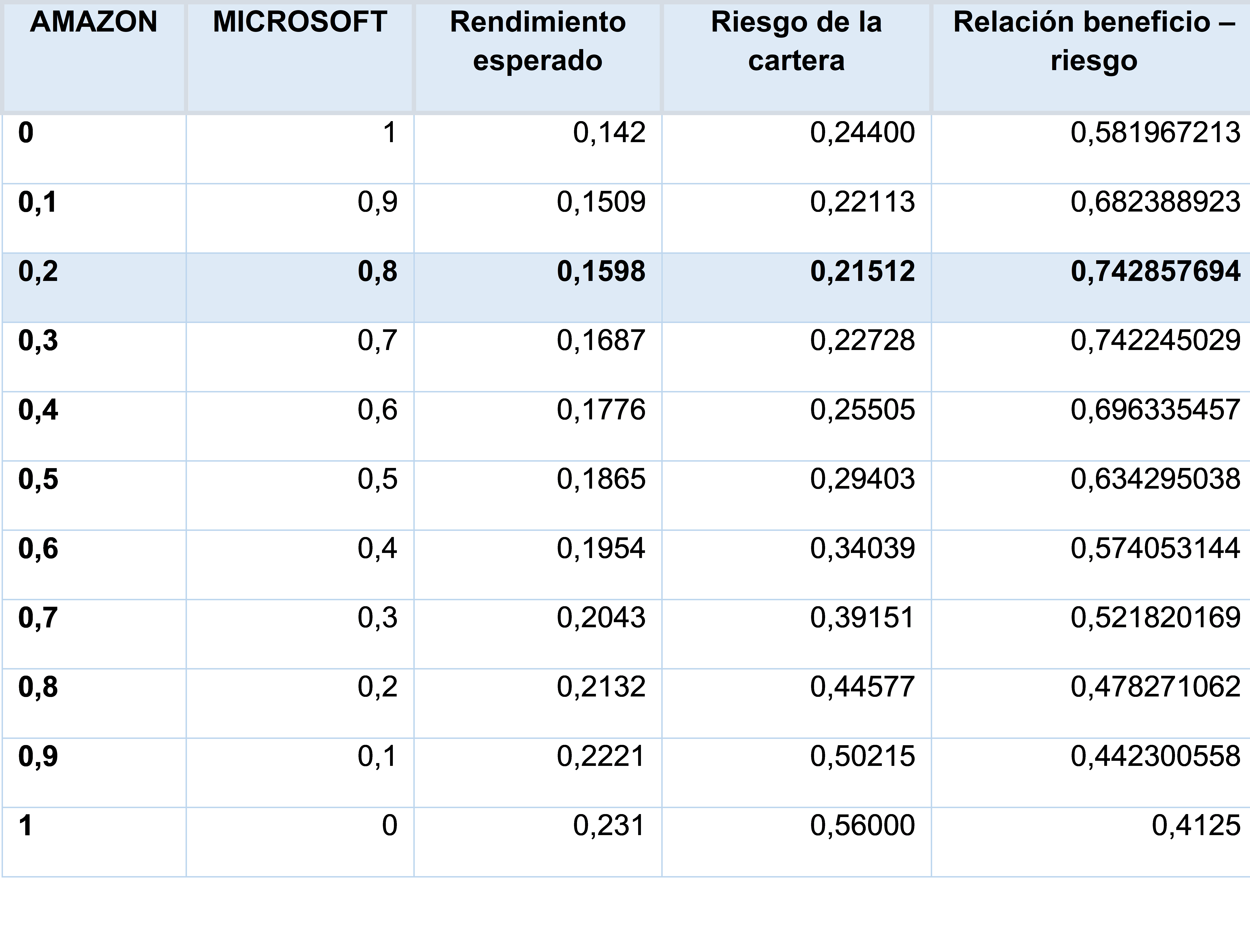
Tabla 2: Distintas combinaciones de betas en la cartera de dos activos. Fuente: elaboración propia

A partir del ejemplo práctico aplicando el Modelo Markowitz, se comprueba que se obtiene un mayor beneficio gracias a la diversificación y no a centrar la inversión en un solo activo.

Bases del modelo

Frontera eficiente

A continuación, se representan dichos casos en un gráfico con la desviación como variable independiente (eje de abscisas) y se pueden observar una serie de puntos que lejos de obtener una función, dan lugar a una hipérbole que permitirá realizar suposiciones para otras combinaciones.

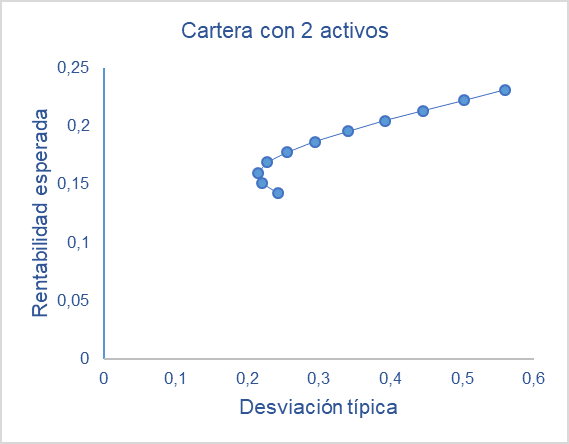
Figura 1. Cartera con 2 activos a partir de los datos anteriores. Fuente: elaboración propia

En vista al ejemplo del gráfico anterior, se observan combinaciones que comparten el mismo nivel de riesgo, pero con rendimientos distintos. Este suceso da nombre al concepto de frontera eficiente, definida como la curva compuesta por todos los puntos con mayor rendimiento y, por ende, los que más interesan. En el caso de realizar el mismo análisis con 3 acciones, se obtendrá un área que estará delimitada superiormente por dicha curva.

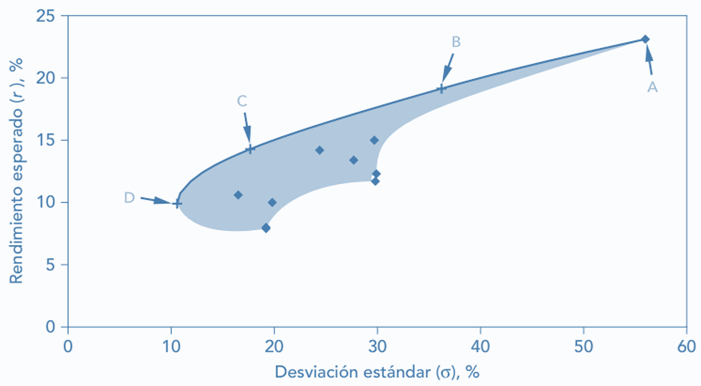
Figura 2. Una cartera con 3 activos. Fuente: (Allen et al. 2010)

De este modo, una vez introducidos los conceptos de rendimiento esperado, desviación y visto un ejemplo gráfico, se formalizan varios conceptos que definen cartera eficiente como:

• Dado un rendimiento esperado determinado, no hay otra cartera que presente un riesgo menor.
• Para un riesgo específico, no hay otra cartera o combinación de activos que permita obtener una rentabilidad mayor.

Capital Allocation Line (CAL)

Hasta ahora, se ha corroborado que la diversificación es más rentable que en lugar de invertir en un solo activo. De la misma forma, sólo se ha tenido en consideración activos con un cierto riesgo, cuando existe la posibilidad de que el riesgo sea cero.

Introduciendo la posibilidad de optar por préstamos y endeudamientos, aparecen otras opciones como las Letras del Tesoro, títulos considerados como los más próximos a tener riesgo cero y, por tanto, un punto sobre el eje de ordenadas en la representación varianza-esperanza. De esta forma, se calcula el rendimiento la cartera óptima en función del de la cartera inicial formada por el inversor y posteriormente, se introduce el activo libre de riesgo. Así pues, se obtiene lo siguiente:

Siendo:

• rentabilidad esperada de la cartera
• proporción en tanto por uno invertida en el activo con riesgo
• rendimiento del activo sin riesgo
• rentabilidad de la cartera del inversor

A su vez, como las proporciones de cada activo son consideradas como variables aleatorias la varianza total se puede expresar en función de la del activo:

 

Reformulando la rentabilidad esperada de la cartera con las ecuaciones anteriores, se puede expresar el beneficio esperado como:

En vista a esta nueva expresión, se puede comprobar que es posible estudiar la relación rentabilidad-riesgo a través de una recta, conocida como Capital Allocation Line (CAL) o Línea de asignación de activos y representa todas las combinaciones (con y sin riesgo) que el inversor puede formar. Al mismo tiempo, en función del riesgo escogido variará la pendiente de dicha recta:

Figura 3. Ejemplo gráfico de distintas CAL en función del riesgo asumido. Fuente: (Moreno y Gutiérrez s. f.)

Para poder elegir el riesgo adecuado y así encontrar la cartera de inversión óptima, es necesario recordar el concepto de frontera eficiente, en donde se habían tenido en cuenta los datos del mercado. Previamente, con cartera de inversión óptima se hace referencia a la combinación riesgo-rendimiento esperado que sea mejor para el inversor. Así pues, si se combina el concepto de frontera eficiente con el de la cartera elaborada por el inversor (reflejada en la Capital Allocation Line), la pendiente óptima será aquella cuya CAL sea tangente a la frontera eficiente.

Ratio de Sharpe

Se ha introducido el concepto de índice o ratio de Sharpe, definida como la pendiente de la Capital Allocation Line. Identificando el numerador como la prima de riesgo, es decir, la diferencia entre el rendimiento esperado de la inversión y la tasa libre de riesgo, la razón de Sharpe se formula de la siguiente forma:

La razón de Sharpe es un indicador utilizado por los inversionistas para estudiar la prima de riesgo con desviaciones elevadas, es decir, un método para poder medir la desviación estándar de la rentabilidad de cualquier fondo individualmente y poder compararla con otros. A mayor razón de Sharpe, mayor pendiente y mejor es la rentabilidad del fondo en relación con la cantidad de riesgo que se ha tomado en la inversión. Por estas razones, resulta interesante estudiar este parámetro y ver cómo, con el paso del tiempo, fondos con menor rentabilidad y volatilidad que otros (más estables en el tiempo), dan un mayor índice de Sharpe.

Este índice lleva el nombre de William Sharpe, quién colaboró conjuntamente con John Lintner y Jack Traynor en la elaboración del modelo de valoración de activos CAPM, basado en el Modelo de Markowitz y que se explicará en profundidad más adelante.

Cómo elegir el riesgo adecuado: curvas de indiferencia

El modelo de Markowitz es un modelo muy intuitivo y con un gran factor personal: el inversor asume un mayor riesgo esperando un mayor beneficio, y a su vez, depende de él el riesgo que esté dispuesto a asumir. Estas dos ideas conducen a la función de utilidad de un inversor que dará lugar a las distintas curvas de indiferencia (monótonas crecientes y convexas) que representarán la aversión al riesgo del inversor.

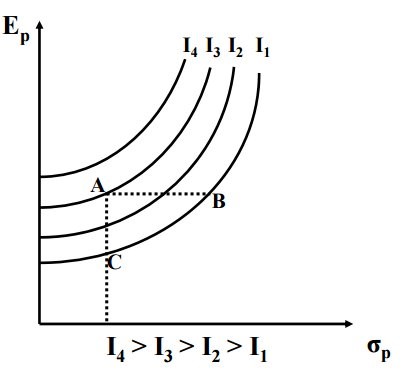
Figura 4. Representación de varias curvas de indiferencia. Fuente: (Hernández 2022)

A un mismo nivel de riesgo se observan distintos rendimientos, por ello cuánto más arriba esté situada la curva más satisfacción obtendrá el inversor. Otra manera de obtener la cartera óptima , aparte de la pendiente de la Capital Allocation Line, consiste en hallar el punto de tangencia entre las curvas de indiferencia y la frontera eficiente. Dicha curva es única para cada inversor al depender de: (i) las combinaciones estimadas de los títulos que conforman la frontera eficiente, (ii) el grado de aversión al riesgo representado por las curvas de indiferencia.

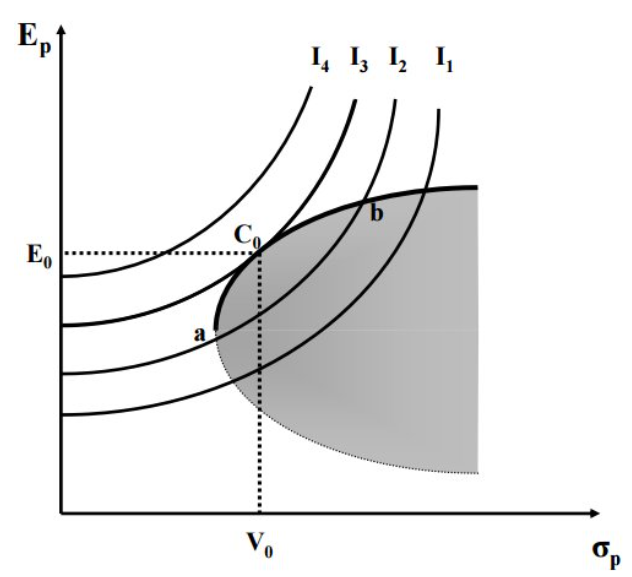
Figura 5. Punto de tangencia entre la frontera eficiente y una curva de indiferencia. Fuente:(Hernández 2022)

Se concluye que dicha unicidad depende íntegramente del inversor, ya sea por el riesgo que decida asumir (curvas de indiferencia) o por la selección de la razón de Sharpe. Sin embargo, para la definición de dichas curvas son necesarias herramientas capaces de cuantificar la actitud del inversor ante el riesgo, algo que no proporciona el modelo. Además, no se han mencionado los costes de transacción ni los impuestos, puesto que el modelo tampoco los incluye. Junto con estas críticas y algunas otras, se discutirá en el capítulo “Críticas a los modelos de gestión de carteras” la veracidad del modelo propuesto por Markowitz.

Un problema de optimización

Para el cálculo de la frontera eficiente es necesario la resolución de un problema de optimización de minimización para lo que es necesario recurrir a la programación cuadrática. Asimismo, es necesario tener en consideración que las variables son aleatorias y que siguen una distribución normal para así poder identificar la media con la rentabilidad esperada y el riesgo con la desviación estándar (Meunier 2021). Planteando las ecuaciones el modelo queda expresado de la siguiente manera:

Un problema de minimización en donde se minimiza la varianza y aparece , la matriz de covarianzas de los activos de dimensiones N x N siendo N el tamaño de la muestra:

Los parámetros  representan la cantidad en tanto por uno invertida en cada activo. De ahí que sea necesario la restricción de no negatividad y que la suma deba de ser igual a 1. Además, en este modelo no son viables la venta en corto, otra razón de la restricción de no negatividad.

A modo aclaratorio y con el objetivo de ayudar a una mayor compresión, para llegar a la expresión de la varianza anterior ha sido necesario tener en consideración que son variables aleatorias independientes y se ha aplicado la propiedad de linealidad:

Hipótesis

Una vez enunciado el modelo, cabe detallar algunas de las hipótesis que lo caracterizan, y que dan lugar a algunas de las críticas que ha recibido el modelo, de los que hablamos aquí. Se pueden clasificar en tres grandes bloques según atiendan a su modelización matemática, al mercado o al inversor.

Respecto a su modelización matemática:

• Los rendimientos se consideran variables aleatorias que siguen una distribución normal y, por consiguiente, se podrán medir probabilidades tomando la media como la rentabilidad esperada y la desviación típica como riesgo.
• Se trata de un modelo estático, los inversores se fijan en un solo periodo que para todos es el mismo. Los activos se consideran con liquidez inmediata una vez finalizado dicho periodo

Respecto al mercado:

• Mercados financieros perfectos, es decir, toda la información está al alcance de todos y no se tienen en cuenta los costes de transacción ni otros factores como la inflación o la liquidez de los activos. Además, se considera a los inversores precio-aceptantes.
• Los títulos son divisibles, es decir, se puede elegir cualquier porcentaje de estos. Y las ventas en corto no están permitidas.

Respecto al inversor:

• El comportamiento de los inversores es racional. En función de su aversión al riesgo, se obtendrá una frontera eficiente diferente buscando maximizar su función de utilidad. Su comportamiento, por tanto, se representa por una función cuadrática que depende solamente del rendimiento esperado.
• Los inversores son aversos al riesgo, es decir, que ante un mismo nivel de rendimiento escogen la cartera que presente menor varianza.

Si te interesa la historia de los ganadores de los Premios Nobeles de Economía, te recomendamos el libro "Una corona de laural naranja", de nuestro amigo José Carlos Gómez Borrero, a quien también puedes conocer por estos artículos del blog:

Milton Friedman.

Hayek y Keynes.

Y por este artículo escrito por él sobre Markowitz:

Finanzas para mortales: Markowitz. 

Notas:

El proyecto value4all es un proyecto divulgativo sin ánimo de lucro. No somos una gestora ni comercializadora de acciones y/o fondos, ni aceptamos publicidad de comercializadoras para preservar la independencia del proyecto.

Los fondos que deposites en renta variable (acciones) no están garantizados. El capital invertido queda por lo tanto sujeto a las subidas y bajadas del mercado. Debes por lo tanto considerar la inversión en Bolsa como un vehículo adecuado para tus ahorros en el largo plazo, esto es, el destino del ahorro que estás seguro de no necesitar en un horizonte de 8-10 años. En caso contrario, el riesgo de que acabes teniendo menos dinero del depositado es muy alto.